常用时域特征
-
峰峰值
-
平均值
-
标准差(均方差,Standard Deviation)
$\sigma = \mathrm{SD}(X) = \sqrt{\frac{1}{N} \sum\limits^N_{n=1} (x_n - \mu)^2}$
当$\mu=0$时,标准差等于均方根RMS。
-
均方根峰峰值
(自己搞的)反应信号的非平稳程度。
-
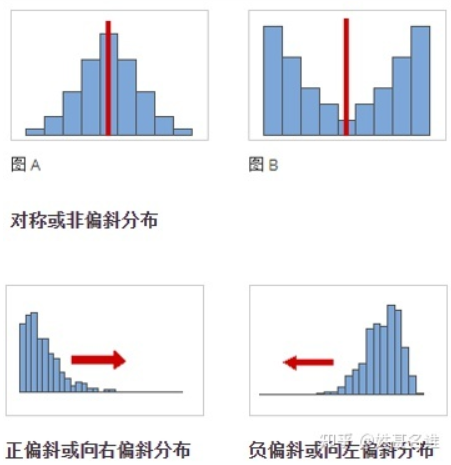
偏度 (Skewness)
$\mathrm{SK} = \frac{\frac{1}{N} \sum\limits^N_{n=1} (x_n - \mu)^3}{\sigma^3}$
反应数据分布的偏斜程度。振动信号一般偏度为0。
-
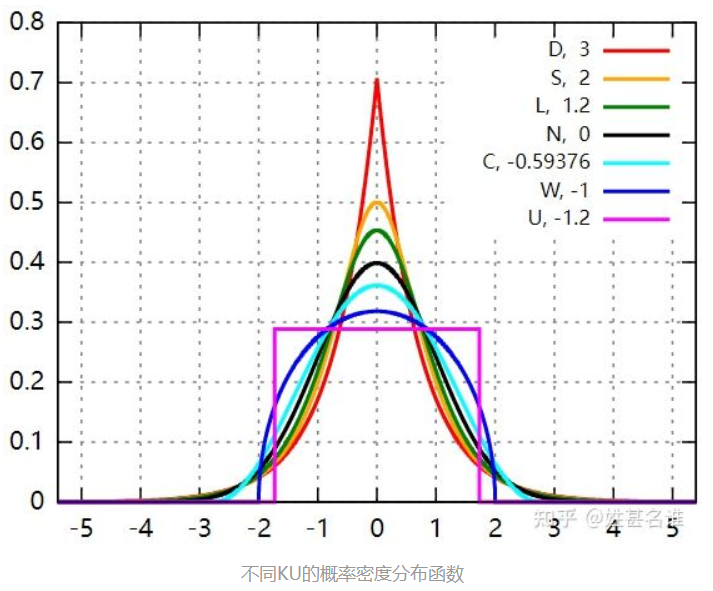
峰度/峭度 (Kurtosis)
$\mathrm{KU} = \frac{\frac{1}{N} \sum\limits^N_{n=1} (x_n - \mu)^4}{\sigma^4} - 3$
反应数据分布相对于正态分布的尖锐程度,数值越大波峰越尖锐。
如果数据分布$\sigma$很小,但满足正态分布,那么即使分布很“窄”很“尖”,KU依然为0。
-
波形指标Shape Indicator, or Form Factor)
$\mathrm{SH}(X) = \frac{\mathrm{RMS}(X)}{\frac{1}{N} \sum^N_{n=1}\lvert{x_n}\rvert}$
-
脉冲指标 (Impulse Indicator)
$\mathrm{IM}(X) = \frac{\mathrm{max}(X)}{\frac{1}{N} \sum^N_{n=1}\lvert{x_n}\rvert}$
信号中冲击越大,IM越大。
-
峰值指标/因数 (Crest Indicator/Factor)
$\mathrm{CR}(X) = \frac{\mathrm{max}\lvert{X}\rvert}{\mathrm{RMS}(X)}$
反应峰值的显著程度。CR=1时无峰。
-
裕度指标 (Clearance Indicator, or Margin Factor)
$\mathrm{CL}(X) = \frac{\mathrm{max}(X)}{\left( \frac{1}{N} \sum^N_{n=1} \sqrt{\lvert{x_n}\rvert} \right)^2}$
IM、CR、CL均为衡量信号中冲击信号程度的指标。
根据观察,IM、CR、CL和SH趋势相关性较强,短时能量rms、标准差、标准差峰峰值、峰峰值趋势相关性较强。
References: